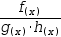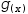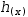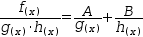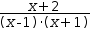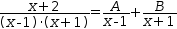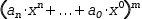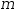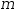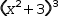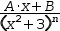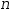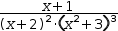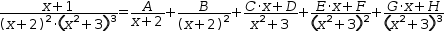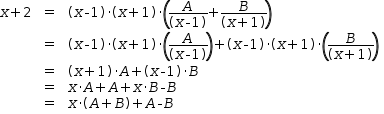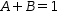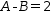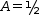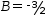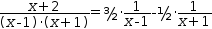3.4.9 Fraction Decomposition
Partial fraction
decomposition is used to change a rational function of
polynomials into a sum of simpler polynomials.
Partial Fraction provides the first step in a sequence of
transformations by rewriting an expression of the form
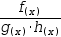 f(x)÷(g(x)⋅h(x))
as the equation
f(x)÷(g(x)⋅h(x))
as the equation
 f(x)÷(g(x)⋅h(x))=e_1(g(x))+e_2(h(x))
where the right side is the expansion of the denominator on the left side.
Note the rewritten equation is useful in this form only if the factors in the
denominator are irreducible polynomials.
f(x)÷(g(x)⋅h(x))=e_1(g(x))+e_2(h(x))
where the right side is the expansion of the denominator on the left side.
Note the rewritten equation is useful in this form only if the factors in the
denominator are irreducible polynomials.
In the simplest case, where 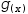 g(x) and
g(x) and 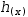 h(x) are polynomials of degree 1,
the expansion is
h(x) are polynomials of degree 1,
the expansion is
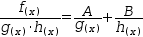 f(x)÷(g(x)⋅h(x))=A÷g(x)+B÷h(x).
For example,
f(x)÷(g(x)⋅h(x))=A÷g(x)+B÷h(x).
For example,
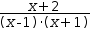 (x+2)÷((x-1)⋅(x+1))
is rewritten as
(x+2)÷((x-1)⋅(x+1))
is rewritten as
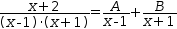 (x+2)÷((x-1)⋅(x+1))=A÷(x-1)+B÷(x+1).
(x+2)÷((x-1)⋅(x+1))=A÷(x-1)+B÷(x+1).
(1)
In the general case, the denominator is a product of exponentiated polynomials
and the number of terms in the expansion is the sum of the exponents.
An exponentiated polynomial is simply a base polynomial raised to some power
like 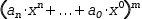 (a_n⋅x^n+..+a_0⋅x^0)^m, which contributes
(a_n⋅x^n+..+a_0⋅x^0)^m, which contributes 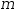 m quotient terms.
The numerator of each quotient term is an abstract polynomial[1]
of degree one less than the base polynomial.
The denominator is the base polynomial raised to successively higher powers until
m quotient terms.
The numerator of each quotient term is an abstract polynomial[1]
of degree one less than the base polynomial.
The denominator is the base polynomial raised to successively higher powers until 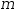 m is reached.
That is, the exponentiated polynomial
m is reached.
That is, the exponentiated polynomial 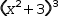 (x^2+3)^3 contributes
three terms of the form
(x^2+3)^3 contributes
three terms of the form 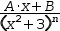 (A⋅x+B)÷(x^2+3)^n where
(A⋅x+B)÷(x^2+3)^n where 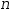 n ranges from 1 to 3
and coefficients are generated so as to be unique to each quotient term.
For example, the expression
n ranges from 1 to 3
and coefficients are generated so as to be unique to each quotient term.
For example, the expression 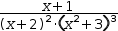 (x+1)÷((x+2)^2⋅(x^2+3)^3)
expands to
(x+1)÷((x+2)^2⋅(x^2+3)^3)
expands to
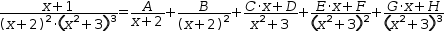 (x+1)÷((x+2)^2⋅(x^2+3)^3)=A÷(x+2)+B÷(x+2)^2+(C⋅x+D)÷(x^2+3)+(E⋅x+F)÷(x^2+3)^2+(G⋅x+H)÷(x^2+3)^3.
(x+1)÷((x+2)^2⋅(x^2+3)^3)=A÷(x+2)+B÷(x+2)^2+(C⋅x+D)÷(x^2+3)+(E⋅x+F)÷(x^2+3)^2+(G⋅x+H)÷(x^2+3)^3.
Because Partial Fraction is just
a first step, and because the subject expression is often
part of a larger expression, the equation is introduced as a separate
expression on the display. The new equation is then subjected to more
manipulations before changes can be made to the original equation. See
§4.4.4
for a complete example.
To continue with example (1) above, the denominator on the left
of (1) is moved to the right side of the equation and
simplified
until an expression in terms of A, B, and x has been reached.
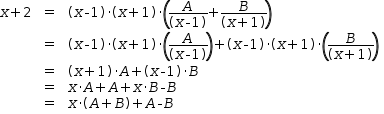 ([(x+2, "=", (x-1)⋅(x+1)⋅(A÷(x-1)+B÷(x+1))), ("", "=", (x-1)⋅(x+1)⋅(A÷(x-1))+(x-1)⋅(x+1)⋅(B÷(x+1))), ("", "=", (x+1)⋅A+(x-1)⋅B), ("", "=", x⋅A+A+x⋅B-B), ("", "=", x⋅(A+B)+A-B)], x+2=x⋅(A+B)+A-B)A
([(x+2, "=", (x-1)⋅(x+1)⋅(A÷(x-1)+B÷(x+1))), ("", "=", (x-1)⋅(x+1)⋅(A÷(x-1))+(x-1)⋅(x+1)⋅(B÷(x+1))), ("", "=", (x+1)⋅A+(x-1)⋅B), ("", "=", x⋅A+A+x⋅B-B), ("", "=", x⋅(A+B)+A-B)], x+2=x⋅(A+B)+A-B)A
From this,
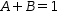 A+B=1
and
A+B=1
and
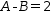 A-B=2, so
A-B=2, so
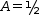 A=1/2
and
A=1/2
and
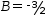 B=-3/2. The final result is
B=-3/2. The final result is
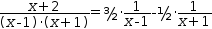 (x+2)÷((x-1)⋅(x+1))=3/2⋅(1÷(x-1))-1/2⋅(1÷(x+1)).
(x+2)÷((x-1)⋅(x+1))=3/2⋅(1÷(x-1))-1/2⋅(1÷(x+1)).
By cross-multiplying, simplifying and factoring, the right side can
be shown to be equal to the left side, proving the decomposition, at least in this case.